cGAN

Conditional Generative Adversarial Nets

1. Generative Adversarial Nets

GAN由两个“对抗性”模型组成：捕获数据分布的生成模型（generative model）$G$，判别模型（discriminative model）$D$ 估计样本来自训练数据而不是 $G$ 的概率。$G$ 和 $D$ 两者可以是非线性映射函数，例如多层感知机。

为了学习在数据 $x$ 上的生成分布 $p_g$，生成器建立了一个从先前噪声分布（prior noise distribution） $p_z(z)$ 到数据空间（data space）的映射函数 $G(z;{\theta }_g)$。同时判别器 $D(x;{\theta }_d)$ 输出一个标量表示 $x$ 来自训练数据而不是 $p_g$​ 的概率。

$G$ 和 $D$ 同时训练：我们调整 $G$ 的参数来最小化 $log(1-D(G(z)))$ ，调整 $D$ 的参数来最小化 $logD(X)$，就好像他们遵循的是带有价值函数 $V(G,D)$ 的双人minimax博弈：

$$\begin{array}{c}\underset{G}{min}\underset{D}{max}V(D,G)={\mathbb{E}}_{x\sim p_{data}(x)}[logD(x)]+{\mathbb{E}}_{z\sim p_z(x)}[log(1-D(G(z)))]\end{array}$$​

对于判别器的输入，无论是真是样本还是预测样本，输入只有 $x$ 和 $G(z)$。在真实的数据中，例如MNIST，照片有10类（0~9手写字识别），对于10类样本，输入仅有一个高斯变量 $z$​​，而没有输入任何其他信息，指望生成器生成相似照片难度较大。输入中真正有帮助预测照片的数据非常少，因此诞生了条件GAN。

2. Conditional Generative Adversarial Nets

如果生成器和判别器都以一些额外的信息 $y$ 为条件，那么 GAN 可以扩展到条件模型。$y$ 可以是任何类型的辅助信息，例如类标签或来自其他模态的数据。我们可以通过将 $y$​ 作为附加输入层同时输入鉴别器和生成器来执行调节。

在生成器中，先验输入噪声 $p_z(z)$ 和 $y$​ 被组合在联合隐藏表示中，并且对抗性训练框架允许在如何组成该隐藏表示方面具有相当大的灵活性。

在判别器中，$x$ 和 $y$​ 被表示为一个判别函数的输入（在本例中再次由MLP体现）。

双人minimax博弈的目标函数为：

$$\begin{array}{c}\underset{G}{min}\underset{D}{max}V(D,G)={\mathbb{E}}_{x\sim p_{data}(x)}[logD(x|y)]+{\mathbb{E}}_{z\sim p_z(x)}[log(1-D(G(z|y)))]\end{array}$$

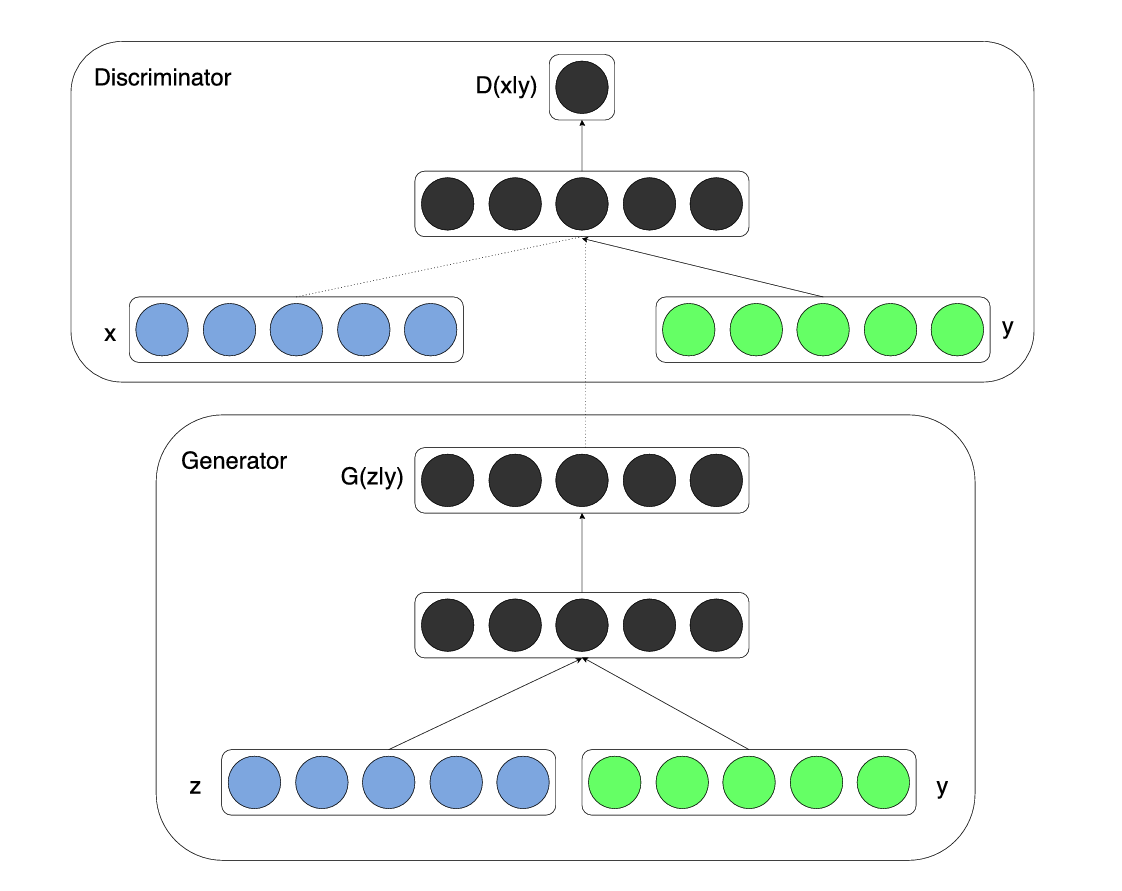
一个简单的条件对抗网络的结构：